Skip Navigation

InitialsDiceBearhttps://github.com/dicebear/dicebearhttps://creativecommons.org/publicdomain/zero/1.0/„Initials” (https://github.com/dicebear/dicebear) by „DiceBear”, licensed under „CC0 1.0” (https://creativecommons.org/publicdomain/zero/1.0/)V

VintageGenious

@ VintageGenious @sh.itjust.works

Posts
7
Comments
307
Joined
2 yr. ago

  • This mom’s son was asking Tesla’s Grok AI chatbot about soccer. It told him to send nude pics, she says

    Jump

  • Your second source is very clear on the fact that "but the presence in documents is not the same as an allegation of criminal conduct" and repeats this information multiple times. I don't say he has nothing to be accountable for, just that this is very far from any proof and people just bend it to fit their narrative.

  • 1X Neo is a $20,000 home robot that will learn chores via teleoperation

    Jump

  • It's so frustrating that they use thorn for voiced th too.

  • 1X Neo is a $20,000 home robot that will learn chores via teleoperation

    Jump

  • To the Korean Linux users: Which distro would you recommend?

    Jump

  • ctrl space is very useful if you have many keyboard layouts

  • "Analog bags" are in. Doomscrolling is out.

    Jump

  • Or any manual task

  • As Microsoft Forces Users to Ditch Windows 10, It Announces That It’s Also Turning Windows 11 into an AI-Controlled Monstrosity

    Jump

  • If you absolutely need to use Windows11, use Tiny11. But for the great majority of users, Zorin/Ubuntu/Mint or Bazzite are best pick

  • Cheapest VPN in the long term for watching movies and tv shows?

    Jump

  • Fines for streaming and not seeding ?

  • What will you do after Android starts restricting FOSS apps?

    Jump

  • But they set a precedent

  • What will you do after Android starts restricting FOSS apps?

    Jump

  • Rename sideloading with installing and play store with baby mode

  • What will you do after Android starts restricting FOSS apps?

    Jump

  • They are kinda the cause. They allowed apple to do this crap and know that it's settled android profits

  • What will you do after Android starts restricting FOSS apps?

    Jump

  • I don't like android 16. I already regret so much updating to Android 15 a few weeks ago: it's onky feature was making notifications huge and replace the monochrome logos with rhe app icon (which is not the one I have on my themed launcher) so it takes more space and is uglier. Same for the new control center: I had to disable it. Horrible locked screen experience too with less icons on top left and ios inspired dynamic island gimmicks.

    Android 16, will be some design choices which are even less customizable I feel (but at least way better than ios broken transparency)

  • What will you do after Android starts restricting FOSS apps?

    Jump

  • Yes it is.

    It will probably be something similar to ios altstore. You would have an app which has a list of your non-playstore apps and repo for their releases and would notify you for upgrades that you would manually have to install (for example I suppose obtainium will implement adb), the setup will be annoying but far far less cumbersome than apple where you have to reboot your device multiple times self sign ipas and refresh once a week otherwise the apps don't load at all. This iOS experience is awful but still doable and non-dev. Android will have a better experience for sure.

  • Google Confirms Non-ADB APK Installs Will Require Developer Registration

    Jump

  • Shizuku

  • Google Confirms Non-ADB APK Installs Will Require Developer Registration

    Jump

  • What is it ?

  • Google Confirms Non-ADB APK Installs Will Require Developer Registration

    Jump

  • We need better Mobile Linux / Android distros

  • Deleted

    Permanently Deleted

    Jump

  • Is wasn't making a proof statement: I wasn't saying that since she's more known others have worse treatment. I based my comment on knowledge of the worse treatment (cited in the other comments).

    Also I wasn't talking about the bed bugs, but about the pulled by hair and forced to kiss flag kind of things.

  • Deleted

    Permanently Deleted

    Jump

  • As a foreign famous activist she probably has a "good" treatment for a detainee. Imagine what the Gazan child hostages go through in Israeli prisons (spoiler: reported electrical shock torture and sexual crimes)

  • OSS PDF editor/markup software recommendations

    Jump

  • Zathura

  • Deleted

    Is there any alternative to Stremio?

    Jump

  • For some reason all streams I try with comet are not cached in my debrid, and it's a rare occurrence on torrentio

  • Open Source @lemmy.ml
    VintageGenious @sh.itjust.works

    Would love to find some kind of rating in Fdroid

  • Technology @lemmy.world
    VintageGenious @sh.itjust.works

    Is there an extensive guide on how to protect kids on the internet?

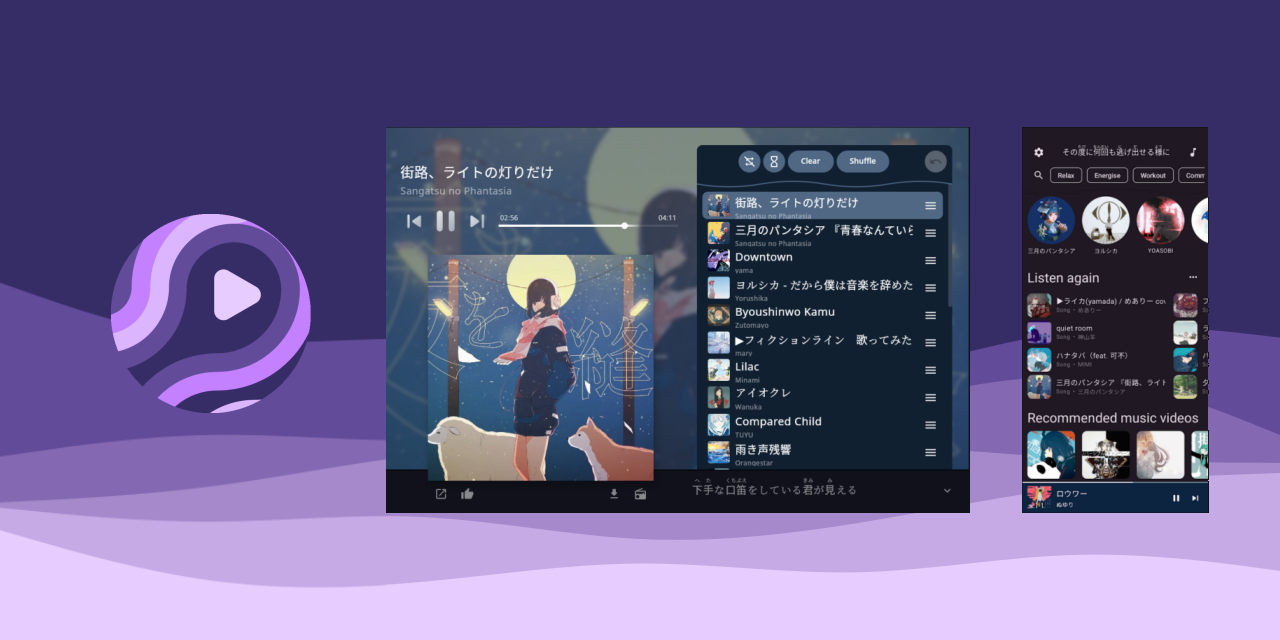
  • Open Source @lemmy.ml
    VintageGenious @sh.itjust.works

    SpMp is one of the prettiest open source android app I've seen. It's a complete free youtube music client

    github.com /toasterofbread/spmp
  • Asklemmy @lemmy.ml
    VintageGenious @sh.itjust.works

    Can you help me collect proofs that Elon Musk is against free speech and other bad things he has done/said ?

  • Fediverse @lemmy.world
    VintageGenious @sh.itjust.works

    Any android client that can do both Lemmy and Mastodon?

  • Linux @lemmy.ml
    VintageGenious @sh.itjust.works

    I just realized all my teachers use ubuntu

  • Piracy: ꜱᴀɪʟ ᴛʜᴇ ʜɪɢʜ ꜱᴇᴀꜱ @lemmy.dbzer0.com
    VintageGenious @sh.itjust.works

    Do you pay for some pirated contents